这是笔者大二上学的课了，现在把之前的笔记整理复习一遍。

部分内容由AI生成。。。

第2章 算法基础

2.1 插入排序

c++代码：

1
2
3
4
5
6
7
8
INSERTION-SORT(A)
for j = 2 to A.length
	key = A[j]
	i = j - 1
	while i > 0 and A[i] > key
		A[i+1] =A[i];
		i = i - 1;
	A[i + 1] = key
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**插入排序
@para array and array's length
下标从0开始
*/
void insertion_sort(int& A, int n){
	for(int j = 1; j < n; j++){
		int key = A[j];
		i = j - 1;
		while(i >= 0 && A[i] > key){
			A[i + 1] = A[i];
			i = i - 1;
		}
	 A[i + 1] = key;
	}
}

2.2 分析算法

2.3 设计算法

分治法：

  1. **分解：**原问题为若干子问题，这些子问题是原问题的规模较小的实例
  2. **解决：**解决这些子问题，递归地求解各子问题
  3. **合并：**合并这些子问题的解成原问题的解

归并排序：

归并排序是一种采用分治法思想的排序算法。它的基本思想是将待排序的序列不断划分为更小的子序列，直到每个子序列只有一个元素，然后再将这些子序列两两合并，最终得到一个有序的序列。

下面是归并排序的C++代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
void merge(int* arr, int p, int q, int r) {
    int n1 = q - p + 1;
    int n2 = r - q;
		//分割成A[p,q],A[q+1,r]
    int* L = new int[n1];
    int* R = new int[n2];

    for (int i = 0; i < n1; i++)
        L[i] = arr[p + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[q + 1 + j];

    int i = 0;
    int j = 0;
    int k = p;

    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }

    delete[] L;
    delete[] R;
}

void mergeSort(int* arr, int p, int r) {
    if (p < r) {
        int q = (p + r) / 2;

        mergeSort(arr, p, q);
        mergeSort(arr, q + 1, r);

        merge(arr, p, q, r);
    }
}

使用归并排序算法可以对数组进行排序。

递归算法的时间复杂度分析

对于递归算法的时间复杂度分析，可以使用递归树来进行推导。递归树的每一层表示递归算法的一次调用，而每一层中的节点表示该层中执行的基本操作次数。

以归并排序算法为例，设原始序列的长度为n。在每次递归调用中，将序列划分为两个子序列，直到每个子序列只有一个元素为止。因此，递归树的高度为log(n)。

在每一层的合并操作中，需要将两个子序列合并为一个有序的序列。合并操作的时间复杂度为O(n)，其中n表示当前层的序列长度。

因此，递归算法的总时间复杂度可以表示为：

1
2
T(n) = 2T(n/2) + O(n)

根据主定理，可以得到归并排序的时间复杂度为O(nlog(n))。

总结：递归算法的时间复杂度分析需要考虑递归树的高度和每层的操作次数，通过递归关系式和主定理来计算总的时间复杂度。

第3章 函数的增长

3.1 渐进记号

算法的渐进记号及含义

在计算机科学中，我们使用渐进记号来描述算法的时间复杂度和空间复杂度。以下是常见的渐进记号及其含义：

  • 大O记号（O）：表示算法的上界，即算法的最坏情况时间复杂度。例如，O(n)表示线性时间复杂度，O(n^2)表示平方时间复杂度。
  • Ω记号（Ω）：表示算法的下界，即算法的最好情况时间复杂度。例如，Ω(n)表示线性时间复杂度，Ω(1)表示常数时间复杂度。
  • Θ记号（Θ）：表示算法的紧密界限，即算法的平均情况时间复杂度。例如，Θ(n)表示线性时间复杂度，Θ(1)表示常数时间复杂度。
  • 小o记号（o）：表示算法的非紧密界限，即算法的最好情况时间复杂度没有上界。例如，o(n)表示比线性时间复杂度更好的复杂度。
  • 小ω记号（ω）：表示算法的非紧密界限，即算法的最坏情况时间复杂度没有下界。例如，ω(n)表示比线性时间复杂度更差的复杂度。

这些渐进记号帮助我们比较和分析不同算法的性能，以便选择最适合特定问题的算法。

第4章 分治策略

在算法中，求解递归式（recurrence relation）的方法有几种常见的技巧。这些方法对于分析算法的时间复杂度非常有帮助。以下是一些常见的求解递归式的方法：

  1. 代入法（Substitution Method）： 这是一种直观的方法，其中你猜测解的形式，然后用数学归纳法证明你的猜测是正确的。
  2. 递归树法（Recurrence Tree Method）： 将递归式表示为一棵树，然后分析这棵树的深度和每个层次的代价。这对于理解递归调用的次数以及每次调用的代价很有帮助。
  3. 主方法（Master Theorem）： 主方法是一种特定形式递归式的通用解法，适用于具有特定形式的分治算法。主方法有三种情况，每种情况对应于不同类型的递归式。

这些方法通常在分析递归算法的时间复杂度时使用。选择哪种方法取决于递归式的形式以及你希望分析的粒度。在学习算法和数据结构时，这些方法通常会在课程中进行详细讲解。

主方法（Master Theorem）是一种用于分析递归算法时间复杂度的技术，特别适用于分治算法。主方法提供了一种简化的方式来确定递归算法的时间复杂度，尤其是对于具有特定形式的递归式。主方法通常用于解决以下形式的递归关系：

T(n)=a⋅T(nb)+f(n)T(n) = a \cdot T\left(\frac{n}{b}\right) + f(n)

其中：

  • T(n)T(n) 是递归函数的时间复杂度。
  • aa 是递归调用的次数。
  • bb 是问题规模缩小的比例。
  • f(n)f(n) 是递归之外的其他操作的时间复杂度。

主方法的一般形式为：

T(n)={Θ(1),n=1a⋅T(nb)+f(n),n=biT(n) = \begin{cases} \Theta (1) & ,n=1\\a \cdot T\left(\frac{n}{b}\right) + f(n)&,n=b^i\end{cases}

其中 a≥1,b>1,f(n)a \geq 1, b > 1 , f(n) 是渐进正函数。

主方法定理提供了对这类递归式的通用解决方案，其中包含了三种情况。这些情况涵盖了许多常见的递归算法。具体的情况取决于 a，b，和 f(n) 的关系。

主方法的三种情况如下：

  1. 情况一： 如果 f(n)f(n) 是 O(nlog⁡ba−ϵ)O(n^{\log_b{a - \epsilon}})（其中 ϵ>0\epsilon > 0），那么 T(n)T(n) 是 Θ(nlog⁡ba)Θ(n^{\log_b{a}})。

  2. 情况二： 如果 f(n)f(n) 是 Θ(nlog⁡ba⋅log⁡kn)Θ(n^{\log_b{a}} \cdot \log^k n)（其中 k≥0k \geq 0），那么 T(n)T(n) 是 Θ(nlog⁡ba⋅log⁡k+1n)Θ(n^{\log_b{a}} \cdot \log^{k+1} n)。

    💡 特别地，如果f(n)=Θ(nlog⁡ba)f(n)=\Theta(n^{\log_ba})，则T(n)=Θ(nlog⁡ba⋅log⁡n)T(n)=\Theta(n^{\log_ba}\cdot \log n)。

  3. 情况三： 如果 f(n)f(n) 是 Ω(nlog⁡ba+ϵ)Ω(n^{\log_b{a + \epsilon}})（其中 ϵ>0\epsilon > 0），如果 af(nb)≤kf(n)a f\left(\frac{n}{b}\right) \leq kf(n)（其中 k<1k < 1）对于足够大的 nn 成立，那么 T(n)T(n) 是 Θ(f(n))Θ(f(n))。

在应用主方法时，首先需要将递归式 T(n)T(n) 表达为上述形式，然后根据 f(n)f(n) 的增长速度与 nlog⁡ban^{\log_b{a}} 进行比较，确定适用于哪一种情况。这样可以更方便地推导递归算法的渐进时间复杂度。

P55 练习4.5-1

  1. T(n)=2T(n/4)+1T(n)=2T(n/4)+1，a=2，b=4，logbalog_ba=12=\frac 12，f(n)=n0f(n)=n^0=O(nlogba−ϵ)=O(n^{log_ba}-\epsilon)，因此T(n)=Θ(n)T(n)=\Theta(\sqrt n)。、
  2. 同理，T(n)=Θ(nlog⁡n)T(n)=\Theta(\sqrt n\log n)
  3. T(n)=Θ(n)T(n)=\Theta(n)
  4. T(n)=Θ(n2)T(n)=\Theta(n^2)

第6章 堆排序

堆、堆排序算法

堆（Heap）是一种数据结构，通常用于实现优先队列。堆分为最大堆和最小堆，最大堆的每个节点的值都大于或等于其子节点，而最小堆的每个节点的值都小于或等于其子节点。

堆排序算法是一种基于堆数据结构的排序方法。它的基本思想是首先将待排序的元素构建成一个最大堆或最小堆，然后依次将堆顶元素（最大值或最小值）取出并调整堆，直到所有元素都被取出，从而得到一个有序序列。

堆排序的步骤如下：

  1. 构建堆：将待排序的元素按顺序插入到堆中，然后依次调整堆，使得每个节点都满足堆的性质。
  2. 堆顶元素与末尾元素交换：将堆顶元素与堆的最后一个元素交换位置。
  3. 调整堆：将交换后的堆顶元素重新调整为堆，保持堆的性质。
  4. 重复步骤2和步骤3，直到堆为空。

堆排序的时间复杂度为O(nlogn)O(n log n)，其中n是待排序元素的个数。它是一种原地排序算法，不需要额外的空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <vector>

using namespace std;

// 调整堆的函数，确保以i为根的子树是一个最大堆
void heapify(vector<int>& arr, int n, int i) {
    int largest = i;    // 初始化最大元素的索引为当前节点
    int left = 2 * i + 1;   // 左子节点的索引
    int right = 2 * i + 2;  // 右子节点的索引

    // 比较左子节点与当前节点的值，找出较大值的索引
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // 比较右子节点与当前节点的值，找出较大值的索引
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 如果最大值的索引不是当前节点，交换它们，并递归调整交换后的子树
    if (largest != i) {
        swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}

// 堆排序主函数
void heapSort(vector<int>& arr) {
    int n = arr.size();

    // 构建最大堆
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
		// 最后一个节点的下标为n-1，则父节点的下标为n/2-1：
		// 若为左节点，n-1为奇，n为偶，（n-1-1）/2=n/2-1
		// 若为右节点，n-1为偶，n为奇，（n-1-2）/2=（n-1）/2-1=[n/2]-1

    // 交换堆顶元素与末尾元素，然后调整堆
    for (int i = n - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

int main() {
    vector<int> arr = {12, 11, 13, 5, 6, 7};
    
    cout << "原始数组：";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    // 调用堆排序函数
    heapSort(arr);

    cout << "排序后的数组：";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

快速排序

快速排序是一种常用的排序算法，它基于分治的思想。其主要步骤包括选择一个基准元素，将数组分成两部分，小于基准的元素放在左边，大于基准的元素放在右边，然后对左右两部分分别递归进行快速排序。

以下是快速排序的基本原理：

  1. 选择基准元素： 从数组中选择一个元素作为基准，通常选择最后一个元素。
  2. 分区： 将数组重新排列，使得小于基准的元素在基准的左边，大于基准的元素在基准的右边。基准元素最终在其最终排序的位置上。
  3. 递归： 对基准元素左右两边的子数组分别递归应用快速排序。

下面是一个简单的C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>

using namespace std;

// 分区函数，选取最后一个元素作为基准值，将小于基准值的元素放在左侧，大于基准值的元素放在右侧
int partition(vector<int>& arr, int low, int high) {
    int pivot = arr[high];  // 选择最后一个元素作为基准值
    int i = low - 1;  // 初始化i为比基准值小的元素的最后一个索引

    // 遍历数组，将小于基准值的元素交换到左侧
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }

    // 将基准值放到最终的位置上
    swap(arr[i + 1], arr[high]);
    return i + 1;
}

// 快速排序主函数
void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        // 找到基准值的位置
        int pivotIndex = partition(arr, low, high);

        // 递归对基准值左右两侧的子数组进行快速排序
        quickSort(arr, low, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, high);
    }
}

int main() {
    vector<int> arr = {12, 11, 13, 5, 6, 7};

    cout << "原始数组：";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    // 调用快速排序函数
    quickSort(arr, 0, arr.size() - 1);

    cout << "排序后的数组：";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

在这个示例中，partition 函数用于对数组进行分区，确定基准值的位置。然后，quickSort 函数递归地对基准值左右两侧的子数组进行快速排序。整体的快速排序算法时间复杂度为O(nlogn)O(n log n)。

快速排序的平均时间复杂度是 O(n log n)。这使得它成为一种非常高效的排序算法。

以下是快速排序时间复杂度的详细分析：

  1. 最好情况：
    • 在最好的情况下，每次选择的基准值都将数组准确地分成两个大小相等的子数组。这导致递归树是平衡的，每一层都有 O(n) 个元素。
    • 在这种情况下，递归的深度是 O(log n)，因为每次都将数组一分为二。
    • 最好情况下的时间复杂度是 O(n log n)。
  2. 最坏情况：
    • 在最坏的情况下，每次选择的基准值都是数组中的最小或最大元素。这导致递归树是不平衡的，其中一个分支没有元素，而另一个分支有 n-1 个元素。
    • 在这种情况下，递归的深度是 O(n)。
    • 最坏情况下的时间复杂度是 O(n^2)。
  3. 平均情况：
    • 平均情况下，快速排序的时间复杂度为 O(n log n)。
    • 这是通过对所有可能的输入情况进行平均计算得出的结果。
    • 在实际应用中，快速排序通常是最好的选择，因为它的平均性能非常好。

总体而言，快速排序在平均情况下的性能较好，但在最坏情况下可能变得不太理想。为了降低最坏情况的发生概率，通常可以采用随机化的方法来选择基准值，或者采用三数中值分割法等策略来选择更好的基准值。这些方法可以提高快速排序的稳定性。

第7章 快速排序

快速排序（Quick Sort）是一种常用的排序算法，它基于分治法（Divide and Conquer）的思想。分治法的基本思想是将问题分成一些小的子问题，递归地解决这些子问题，然后合并其结果以解决原始问题。

以下是快速排序的详细过程：

  1. 选择枢纽元素： 从数组中选择一个元素作为枢纽元素（pivot）。通常选择数组的最后一个元素，但也可以选择其他位置的元素。
  2. 分割阶段： 将数组中的元素重新排列，使得小于枢纽元素的元素位于其左侧，而大于枢纽元素的元素位于其右侧。枢纽元素此时已经处于正确的位置，称为分割点（pivot point）。
    • 设置两个指针，一个指向当前处理的元素，一个指向数组的起始位置。开始时，两个指针重合。
    • 从数组的起始位置遍历到倒数第二个元素，将小于枢纽元素的元素交换到左侧，同时移动指针。
    • 最后，将枢纽元素交换到正确的位置，使得左侧的元素都小于它，右侧的元素都大于它。
    • 分割点的位置确定后，数组被分成两个部分，分别对这两个部分递归地应用快速排序。
  3. 递归排序： 对分割点左右两侧的子数组分别进行递归排序。
  4. 合并： 递归排序的最终结果就是整个数组有序。由于分治法的特性，各个子数组在排序完成后，整个数组也就自然有序了。

下面是一个简单的例子，演示了快速排序的过程：

假设数组为 [12, 7, 11, 8, 5, 3, 2, 10]，选择最后一个元素 10 作为枢纽元素：

  1. 初始数组：[12, 7, 11, 8, 5, 3, 2, 10]
  2. 枢纽元素选择为 10，分割点位置：4
  3. 分割后的数组：[7, 8, 5, 3, 2, 10, 12, 11]
  4. 递归排序左侧子数组 [7, 8, 5, 3, 2]
  5. 递归排序右侧子数组 [12, 11]
  6. 最终有序数组：[2, 3, 5, 7, 8, 10, 11, 12]

这就是快速排序的基本思想和实现过程。它的平均时间复杂度为 O(nlogn)O(n log n)，其中 nn 是数组的长度。快速排序在实践中表现出色，被广泛应用于各种应用场景。

快速排序（Quick Sort）是一种常用的排序算法，属于分治法的一种。以下是一个简单的C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>

// 函数声明
int partition(std::vector<int>& arr, int low, int high);
void quickSort(std::vector<int>& arr, int low, int high);

// 分割数组并返回分割点
int partition(std::vector<int>& arr, int low, int high) {
    int pivot = arr[high];  // 选择数组最后一个元素作为枢纽元素
    int i = (low - 1);      // 设置分割点的初始位置

    // 重新排列数组，将小于枢纽元素的元素移到左侧，大于的移到右侧
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            std::swap(arr[i], arr[j]);
        }
    }

    // 将枢纽元素放到正确的位置
    std::swap(arr[i + 1], arr[high]);
    return (i + 1);
}

// 递归实现快速排序
void quickSort(std::vector<int>& arr, int low, int high) {
    if (low < high) {
        // 获取分割点
        int pi = partition(arr, low, high);

        // 对分割点左右两侧的子数组进行递归排序
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    std::vector<int> arr = {12, 7, 11, 8, 5, 3, 2, 10};
    int n = arr.size();

    std::cout << "原始数组: ";
    for (int i = 0; i < n; i++)
        std::cout << arr[i] << " ";

    quickSort(arr, 0, n - 1);

    std::cout << "\\n排序后的数组: ";
    for (int i = 0; i < n; i++)
        std::cout << arr[i] << " ";

    return 0;
}

这个程序演示了快速排序的基本原理，通过递归调用对数组进行排序。希望对你有帮助！如果有任何问题，欢迎提问。

第15章 动态规划

动态规划（Dynamic Programming，简称DP）是一种解决复杂问题的优化方法，它通常用于解决具有重叠子问题和最优子结构性质的问题。动态规划的核心思想是将问题分解成子问题，并通过存储子问题的解来避免重复计算，从而提高效率。

动态规划的一般步骤包括：

  1. 定义子问题： 将原问题分解成更小的子问题。
  2. 找到状态转移方程： 定义问题的状态以及状态之间的关系，即如何通过已解决的子问题的解来计算原问题的解。
  3. 解决基本问题： 找到最小子问题的解，通常是通过初始条件或边界条件来定义的。
  4. 自底向上或自顶向下求解： 动态规划可以采用自底向上的迭代方法，也可以采用自顶向下的递归方法。

动态规划常见的应用场景包括：

  • 最优子结构： 问题的最优解可以通过子问题的最优解来构造。
  • 重叠子问题： 问题可以被分解成一些相同的子问题，这些子问题在求解过程中会被重复计算。
  • 状态转移方程： 问题的解可以通过状态之间的转移得到。

一些经典的动态规划问题包括：

  1. 斐波那契数列： 寻找第n个斐波那契数。
  2. 最长递增子序列： 找到给定数组中的最长递增子序列的长度。
  3. 背包问题： 给定一组物品的重量和价值，确定如何选择这些物品以获得最大的总价值，在限定总重量的情况下。
  4. 编辑距离： 计算两个字符串之间的最小编辑操作数，如插入、删除、替换，使得一个字符串变成另一个字符串。
  5. 最短路径问题： 在图中找到从一个顶点到另一个顶点的最短路径。

下面是一个简单的动态规划示例，计算斐波那契数列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <vector>

using namespace std;

int fibonacci(int n) {
    vector<int> dp(n + 1, 0);
    dp[0] = 0;
    dp[1] = 1;

    for (int i = 2; i <= n; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

int main() {
    int n = 6;
    cout << "Fibonacci(" << n << ") = " << fibonacci(n) << endl;

    return 0;
}

在这个示例中，dp 数组存储了计算过的子问题的解，通过迭代的方式自底向上计算斐波那契数列。

经典动态规划问题

  • 钢条切割问题

    钢条切割问题是动态规划中经典的例子之一。问题的描述是给定一段长度为n的钢条和一个价格表，如何切割钢条使得销售收益最大。

    下面是一个简化的问题描述：

    • 钢条长度为i的价格为p[i]。
    • 如果要切割钢条，会有不同的价格。

    问题的目标是找到一种切割方式，使得销售收益最大。这是一个典型的动态规划问题。

    下面是一个简单的C++代码，用于解决钢条切割问题：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    #include <iostream>
    #include <vector>
    #include <algorithm>

    using namespace std;

    int cutRod(vector<int>& price, int n) {
        vector<int> dp(n + 1, 0);

        for (int i = 1; i <= n; ++i) { // 钢条为i时
            int maxVal = INT_MIN;
            for (int j = 1; j <= i; ++j) { // 切割成j和i-j两段
                maxVal = max(maxVal, price[j] + dp[i - j]);
            }
            dp[i] = maxVal;
        }

        return dp[n];
    }

    int main() {
        vector<int> price = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};  // 价格表，下标对应钢条长度
        int n = 8;  // 钢条长度

        int maxRevenue = cutRod(price, n);

        cout << "Maximum revenue for a rod of length " << n << ": " << maxRevenue << endl;

        return 0;
    }

    这个例子中，price向量表示每个长度的钢条的价格，cutRod函数通过动态规划计算最大的销售收益。在主函数中，我们可以改变钢条长度和价格表，以测试不同情况下的最大收益。

    请注意，这只是钢条切割问题的一种解法，具体问题和实际应用可能需要适当的调整。

第17章 摊还分析

什么是摊还分析？

摊还分析其实就是评价某一个操作的代价，方法就是求某数据结构中一系列操作的平均时间。

摊还分析与概率无关，可以保证某一系列操作在最坏情况下的平均性能。

  1. 聚合分析：一个n个操作的序列最坏情况下花费的总时间为T(n)T(n)。在最坏情况下，每个操作的平均代价，或摊还代价为T(n)/nT(n)/n。

  2. 核算法（accounting method）

  3. 势能法

第22章 基本的图算法

图的表示

有两种主要的图表示方法：

  1. 邻接矩阵： 邻接矩阵是一个二维数组，用于表示图中节点之间的关系。如果图是有向的，邻接矩阵是一个方阵。对于无向图，邻接矩阵是对称的。矩阵的行和列代表图中的节点，矩阵中的值表示对应节点之间是否有边以及边的权重。
  2. 邻接列表： 邻接列表是一种以列表的形式表示图的方法。对于每个节点，都有一个与之相邻的节点列表。这种表示方法更节省空间，特别是在稀疏图（边相对较少）的情况下。

在实际编程中，选择哪种图表示方法取决于具体问题的要求和图的规模。如果图是稠密的（边相对较多），邻接矩阵可能更适合。而对于稀疏图，邻接列表可能更有效。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <vector>

using namespace std;

int n, m;
vector<bool> vis;
vector<vector<bool> > adj;

bool find_edge(int u, int v) { return adj[u][v]; }

void dfs(int u) {
  if (vis[u]) return;
  vis[u] = true;
  for (int v = 1; v <= n; ++v) {
    if (adj[u][v]) {
      dfs(v);
    }
  }
}

int main() {
  cin >> n >> m;

  vis.resize(n + 1, false);
  adj.resize(n + 1, vector<bool>(n + 1, false));

  for (int i = 1; i <= m; ++i) {
    int u, v;
    cin >> u >> v;
    adj[u][v] = true;
  }

  return 0;
}

广度优先搜索、深度优先搜索

广度优先搜索（Breadth-First Search，简称BFS）是一种图搜索算法，用于遍历或搜索图的结构。以下是一个简单的C++实现，假设图的表示是邻接列表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <iostream>
#include <queue>
#include <vector>

using namespace std;

class Graph {
private:
    int vertices;
    vector<vector<int>> adjacencyList;

public:
    Graph(int v) : vertices(v), adjacencyList(v) {}

    void addEdge(int v, int w) {
        adjacencyList[v].push_back(w);
        adjacencyList[w].push_back(v);  // undirected graph
    }

    void BFS(int startVertex) {
        vector<bool> visited(vertices, false);  // Mark all vertices as not visited
        queue<int> q;

        visited[startVertex] = true;
        q.push(startVertex);

        while (!q.empty()) {
            int currentVertex = q.front();
            cout << currentVertex << " ";
            q.pop();

            for (int neighbor : adjacencyList[currentVertex]) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    q.push(neighbor);
                }
            }
        }
    }

    void DFS(int startVertex) {
        vector<bool> visited(vertices, false);  // Mark all vertices as not visited
        stack<int> s;

        visited[startVertex] = true;
        s.push(startVertex);

        while (!s.empty()) {
            int currentVertex = s.top();
            cout << currentVertex << " ";
            s.pop();

            for (int neighbor : adjacencyList[currentVertex]) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    s.push(neighbor);
                }
            }
        }
    }

};

int main() {
    // Example usage
    Graph g(6);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 4);
    g.addEdge(3, 5);

    cout << "BFS starting from vertex 0: ";
    g.BFS(0);
    cout << endl;
    cout << "DFS starting from vertex 0: ";
    g.DFS(0);

    return 0;
}

在这个例子中，Graph 类表示图，addEdge 方法用于添加边，而BFS 方法实现了广度优先搜索。你可以根据实际情况修改图的表示和算法的实现。这个示例是基于邻接列表的图表示。如果你使用邻接矩阵或其他表示方法，相应的数据结构和算法可能会有所不同。

💡 重点：DFS（接下来的拓扑排序要用到）

算法特点

  • 深度优先搜索是一个递归的过程。
    • 首先，选定一个出发点后进行遍历，如果有邻接的未被访问过的节点则继续前进。
    • 若不能继续前进，则回退一步再前进
    • 若回退一步仍然不能前进，则连续回退至可以前进的位置为止。
    • 重复此过程，直到所有与选定点相通的所有顶点都被遍历。
  • 深度优先搜索是递归过程，带有回退操作，因此需要使用栈存储访问的路径信息。当访问到的当前顶点没有可以前进的邻接顶点时，需要进行出栈操作，将当前位置回退至出栈元素位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// 邻接表的深度有限递归算法

#define TRUE 1
#define FALSE 0
#define MAX 256

typedef int Boolean; // 这里我们定义Boolean为布尔类型，其值为TRUE或FALSE
Boolean visited[MAX]; // 访问标志的数组

void DFS(GraphAdjList GL, int i)
{
  EdgeNode *p;
  
  visited[i] = TRUE;
  printf("%c " GL->adjList[i].data);
  p = GL->adjList[i].firstEdge;
  
  while(p)
  {
    if( !visited[p->adjvex] )
    {
      DFS(GL, p->adjvex);
    }
    p = p->next;
  }
}

// 邻接表的深度遍历操作
void DFSTraverse(GraphAdjList GL)
{
  int i;
  
  for( i=0; i < GL->numVertexes; i++ )
  {
    visited[i] = FALSE; // 初始化所有顶点状态都是未访问过状态
  }
  
  for( i=0; i < GL->numVertexes; i++ )
  {
    if( !visited[i] ) // 若是连通图，只会执行一次
    {
      DFS(GL, i);
    }
  }
}

拓扑排序

Untitled

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int n, m;
vector<int> G[MAXN];
int in[MAXN];  // 存储每个结点的入度

bool toposort() {
  vector<int> L;
  queue<int> S;
  for (int i = 1; i <= n; i++)
    if (in[i] == 0) S.push(i);
  while (!S.empty()) {
    int u = S.front();
    S.pop();
    L.push_back(u);
    for (auto v : G[u]) {
      if (--in[v] == 0) {
        S.push(v);
      }
    }
  }
  if (L.size() == n) {
    for (auto i : L) cout << i << ' ';
    return true;
  } else {
    return false;
  }
}

DFS实现拓扑排序

基本图算法(二) 拓扑排序_拓扑排序算法-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 边的结构体，表示图中的边
struct EdgeNode {
    int adjVertex;       // 相邻顶点的索引
    // 其他边的信息，例如权重等，根据实际情况添加
    // ...
    EdgeNode* next;      // 指向下一条边的指针
};

// 顶点的结构体，表示图中的顶点
struct VertexNode {
    // 顶点的其他信息，例如顶点值等，根据实际情况添加
    // ...
    EdgeNode* firstEdge;  // 指向第一条与该顶点相邻的边的指针
};

// 图的结构体，使用邻接表表示
struct ALGraph {
    std::vector<VertexNode> vertices;  // 顶点数组，每个元素表示一个顶点
    // 其他图的信息，例如顶点数、边数等，根据实际情况添加
    // ...
};

访问时三个状态：

⋅「未搜索」：我们还没有搜索到这个节点，用0表示，标记为白色；

⋅「搜索中」：我们搜索过这个节点，但还没有回溯到该节点，即该节点还没有入栈，还有相邻的节点没有搜索完成，用1表示，标记为灰色；

⋅「已完成」：我们搜索过并且回溯过这个节点，即该节点已经入栈，并且所有该节点的相邻节点都出现在栈的更底部的位置，满足拓扑排序的要求，用2表示，标记为绿色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 判断有向图中是否有环
bool valid;
// 栈
int* stack;
int top;

void dfs(ALGraph G, int* visited, int u) {
	// 设置当前节点状态为访问中(1)
	visited[u] = 1;
	// 访问节点u的所有临节点v
	EdgeNode* e = G.vertices[u].firstEdge;
	while (e) {
		int v = e->adjvex;
		if (!visited[v]) 
			dfs(G, visited, v);
		// 如果节点v的状态为搜索中(1),则有向图有环
		else if (visited[v] == 1) {
			valid = false;
			return;
		}
		e = e->next;
	}

	// 设置当前节点状态为已访问(2)并入栈
	visited[u] = 2;
	stack[top++] = u;
}

void TopologicalSort(ALGraph G) {
	// 设置每个顶点的状态为未搜索(0)
	int* visited = calloc(G.vertexNum, sizeof(int));
	stack = malloc(sizeof(int) * G.vertexNum);
	valid = true;
	for (int i = 0; i < G.vertexNum; i++) {
		if (!valid)   break;
		if (!visited[i]) {
			dfs(G, visited, i);
		}
	}
	if (!valid)
		printf("There are loops in Graph\n");
	while (top) 
		printf("%d ", stack[--top]);
}

第23章 最小生成树

一、最小生成树是什么？

最小生成树，全称是Minimum Spanning Tree，简称为MST，其具体定义如下：
  在一给定的无向图G=(V,E)G = ( V , E )中，(u,v)( u , v ) 代表连接顶点 uu 与顶点vv 的边，而w(u,v)w ( u , v ) 代表此边的权重。若存在TT 为EE 的子集且为无循环图，使得联通所有结点的的w(T)w ( T ) 最小，则此TT 为GG 的最小生成树。即：
w(t)=∑(u,v)∈tw(u,v)w(t)=\underset{(u,v)\in t}{\sum}w(u,v)

因此，最小生成树其实是最小权重生成树的简称。

二、最小生成树的算法

1. Kurskal算法

俗称“加边法”，算法复杂度：O(Elog⁡V)O(E\log V),其中E是边的数量，V是顶点数量，适合于边比较少的【稀疏图】。

Kruskal 算法提供一种在 O(Elog⁡V)O(E\log V) 运行时间确定最小生成树的方案。Kruskal 算法基于贪心算法（Greedy Algorithm）的思想进行设计，其选择的贪心策略就是，每次都选择权重最小的但未形成环路的边加入到生成树中。实现利用【并查集】合并和检查是否形成环。其算法结构如下：

👉

1、将所有的边按照权重非递减排序；
2、选择最小权重的边，判断是否其在当前的生成树中形成了一个环路。
如果环路没有形成，则将该边加入树中，否则放弃。
3、重复步骤 2，直到有 V – 1 条边在生成树中。

Kruskal算法是一种用于求解最小生成树（Minimum Spanning Tree）的贪心算法。以下是一个简单的C++实现，假设图是以边的形式表示的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 边的结构体，包含起点、终点和权重
struct Edge {
    int start;
    int end;
    int weight;

    // 比较函数，用于排序
    bool operator<(const Edge& other) const {
        return weight < other.weight;
    }
};

// 并查集（Union-Find）的实现
class UnionFind {
public:
    UnionFind(int size) {
        parent.resize(size);
        rank.resize(size, 0);
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
        }
    }

    // 查找根节点
    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 合并两个集合
    void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY) {
            // 将rank较小的树连接到rank较大的树上
            if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else {
                // 如果rank相等，则选择一个作为根，并增加其rank
                parent[rootX] = rootY;
                rank[rootY]++;
            }
        }
    }

private:
    vector<int> parent;
    vector<int> rank;
};

// Kruskal算法实现
vector<Edge> kruskal(vector<Edge>& edges, int numVertices) {
    // 将边按权重升序排序
    sort(edges.begin(), edges.end());

    // 初始化并查集
    UnionFind uf(numVertices);

    vector<Edge> result; // 存储最小生成树的边

    for (const Edge& edge : edges) {
        // 如果加入这条边不会形成环，则加入最小生成树
        if (uf.find(edge.start) != uf.find(edge.end)) {
            result.push_back(edge);
            uf.unite(edge.start, edge.end);
        }
    }

    return result;
}

// 不使用类：
struct Edge {
    int src, dest, weight;
};

bool compareEdges(const Edge& a, const Edge& b) {
    return a.weight < b.weight;
}

int findParent(int u, vector<int>& parent) {
    return (parent[u] == u) ? u : (parent[u] = findParent(parent[u], parent));
}

void merge(int u, int v, vector<int>& parent, vector<int>& rank) {
    int rootU = findParent(u, parent);
    int rootV = findParent(v, parent);

    if (rank[rootU] > rank[rootV]) {
        parent[rootV] = rootU;
    } else if (rank[rootU] < rank[rootV]) {
        parent[rootU] = rootV;
    } else {
        parent[rootV] = rootU;
        rank[rootU]++;
    }
}

vector<Edge> kruskal(vector<Edge>& edges, int n) {
    vector<Edge> result;
    sort(edges.begin(), edges.end(), compareEdges);

    vector<int> parent(n);
    vector<int> rank(n, 0);

    for (int i = 0; i < n; ++i) {
        parent[i] = i;
    }

    for (const Edge& edge : edges) {
        int rootSrc = findParent(edge.src, parent);
        int rootDest = findParent(edge.dest, parent);

        if (rootSrc != rootDest) {
            result.push_back(edge);
            merge(rootSrc, rootDest, parent, rank);
        }
    }

    return result;
}

int main() {
    // 示例图的边集合，包括起点、终点和权重
    vector<Edge> edges = {
        {0, 1, 2},
        {0, 2, 4},
        {1, 2, 1},
        {1, 3, 7},
        {2, 3, 3}
        // 可以根据需要添加更多的边
    };

    // 图的顶点数
    int numVertices = 4;

    // 调用Kruskal算法求最小生成树
    vector<Edge> minSpanningTree = kruskal(edges, numVertices);

    // 输出最小生成树的边
    cout << "Edges in the Minimum Spanning Tree:\\n";
    for (const Edge& edge : minSpanningTree) {
        cout << edge.start << " - " << edge.end << " : " << edge.weight << "\\n";
    }

    return 0;
}

这个示例实现了一个简单的Kruskal算法，你可以根据需要修改边的集合和顶点数。在这个例子中，Edge结构体表示图的边，UnionFind类表示并查集，kruskal函数执行Kruskal算法，最后在main函数中输出最小生成树的边。

2. Prim算法

俗称“加点法”，算法复杂度：O(V2)O(V^2) ,其中V是顶点数量，适合于边比较多，顶点较少的【稠密图】。

💡 从图G=V,EG={V,E}中的某一顶点U0U_0出发，选择与它关联的具有最小权值的边(U0,v)(U_0,v)，将其顶点加入到生成树的顶点集合UU中。以后每一步从一个顶点在UU中，而另一个顶点不在UU中的各条边中选择权值最小的边(u,v)u,v),把它的顶点加入到集合U中。如此继续下去，直到网中的所有顶点都加入到生成树顶点集合U中为止。

Prim算法是一种用于求解最小生成树（Minimum Spanning Tree）的贪心算法，与Kruskal算法类似，但实现方式略有不同。Prim算法从一个初始顶点开始，逐步选择连接到当前生成树的最短边，直到生成树覆盖了图中所有的顶点。以下是Prim算法的详细解释和C++实现示例：

Prim算法步骤：

  1. 选择一个起始顶点作为初始生成树。
  2. 将选择的顶点标记为已访问。
  3. 在与当前生成树相邻的所有未访问顶点中，选择权值最小的边。
  4. 将选择的边加入生成树，将连接的顶点标记为已访问。
  5. 重复步骤3和步骤4，直到生成树包含了图中的所有顶点。

Prim算法C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <iostream>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

// 定义边的结构体
struct Edge {
    int dest, weight;
};

// 定义用于最小堆的比较函数
struct Compare {
    bool operator()(const Edge& a, const Edge& b) {
        return a.weight > b.weight;
    }
};

// Prim算法实现
vector<Edge> prim(vector<vector<Edge>>& graph, int start) {
    int n = graph.size();
    vector<bool> visited(n, false);
    vector<Edge> result;
    priority_queue<Edge, vector<Edge>, Compare> pq;

    // 将起始顶点标记为已访问
    visited[start] = true;

    // 将起始顶点的所有边加入最小堆
    for (const Edge& edge : graph[start]) {
        pq.push(edge);
    }

    while (!pq.empty()) {
        // 从最小堆中取出权值最小的边
        Edge current = pq.top();
        pq.pop();

        int dest = current.dest;
        int weight = current.weight;

        // 如果目标顶点未访问，则将边加入生成树，并将目标顶点标记为已访问
        if (!visited[dest]) {
            result.push_back({dest, weight});
            visited[dest] = true;

            // 将目标顶点的所有边加入最小堆
            for (const Edge& edge : graph[dest]) {
                pq.push(edge);
            }
        }
    }

    return result;
}

int main() {
    int n = 5; // 节点数
    vector<vector<Edge>> graph(n);

    // 添加边信息（无向图）
    graph[0].push_back({1, 2});
    graph[0].push_back({3, 6});
    graph[1].push_back({0, 2});
    graph[1].push_back({2, 3});
    graph[1].push_back({3, 8});
    graph[2].push_back({1, 3});
    graph[2].push_back({4, 5});
    graph[3].push_back({0, 6});
    graph[3].push_back({1, 8});
    graph[4].push_back({2, 5});

    int startVertex = 0; // 选择起始顶点

    vector<Edge> result = prim(graph, startVertex);

    // 输出最小生成树的边
    cout << "Edges in the Minimum Spanning Tree:\\n";
    for (const Edge& edge : result) {
        cout << startVertex << " - " << edge.dest << " : " << edge.weight << "\\n";
    }

    return 0;
}

这是一个简单的Prim算法实现示例。请注意，Prim算法的实现可能因图的表示方式而异，上述代码使用邻接表来表示图。在实际应用中，你可能需要根据具体情况进行适当的修改。

第24章 单源最短路径

我们给定一个带权重的有向图G(V,E)G(V,E) 和权重函数w:E→Rw:E\to \bm{R} ，该权重函数将每条边映射到实数值的权重上。图中一条路径p=⟨v0,v1,⋯ ,vk⟩p=\langle v_0,v_1,\cdots,v_k\rangle 的权重w(p)w(p)是构成该路径的所有边的权重之和：

w(p)=∑i=1kw(vi−1,vi)w(p)=\sum_{i=1}^kw(v_{i-1},v_i)

松弛操作（relaxation）

维持一个属性v.dv.d，用来记录从源节点ss到节点vv的最短路径的上界。

1
2
3
4
5
6
7
8
9
10
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex v \belong G.V
	v.d = \infty 
	v.\pi = NIL
s.d = 0

RELAX(u,v,w)
if v.d>u.d+w(u.v)
	v.d = u.d+w(u,v)
	v.\pi = u

Bellman-Ford算法

Bellman-Ford算法是一种用于解决单源最短路径问题的算法，它可以处理带有负权边的图。以下是Bellman-Ford算法的详细说明以及一个简单的C++实现。

Bellman-Ford算法简介：

Bellman-Ford算法的基本思想是通过不断迭代，更新从源节点到其他节点的最短路径估计值，直到找到最短路径或者确定图中存在负权环。

算法步骤：

  1. 初始化：将源节点的最短路径估计值设为0，其他节点的最短路径估计值设为正无穷大。
  2. 进行∣V∣−1|V| - 1轮迭代，其中∣V∣|V|是图中节点的数量。
  3. 在每一轮迭代中，遍历图中的所有边，更新节点的最短路径估计值。
  4. 如果在∣V∣−1|V| - 1轮迭代后，仍然存在可以松弛的边，说明图中存在负权环。

💡 时间复杂度：O(VE)O(VE)

C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <vector>

using namespace std;

struct Edge {
    int src, dest, weight;
};

bool bellmanFord(vector<Edge>& edges, int V, int E, int src) {
    vector<int> distance(V, INT_MAX);
    distance[src] = 0;

    // Relaxation step
    for (int i = 1; i <= V - 1; ++i) {
        for (int j = 0; j < E; ++j) {
            int u = edges[j].src;
            int v = edges[j].dest;
            int w = edges[j].weight;
            if (distance[u] != INT_MAX && distance[u] + w < distance[v]) {
                distance[v] = distance[u] + w;
            }
        }
    }

    // Check for negative-weight cycles
    for (int i = 0; i < E; ++i) {
        int u = edges[i].src;
        int v = edges[i].dest;
        int w = edges[i].weight;
        if (distance[u] != INT_MAX && distance[u] + w < distance[v]) {
            cout << "Graph contains negative weight cycle!" << endl;
            return false;
        }
    }

    // Print the result
    cout << "Shortest distances from source " << src << " to all other vertices:" << endl;
    for (int i = 0; i < V; ++i) {
        cout << "Vertex " << i << ": " << distance[i] << endl;
    }
    return true;
}

int main() {
    int V, E; // V is the number of vertices, E is the number of edges
    cout << "Enter the number of vertices and edges: ";
    cin >> V >> E;

    vector<Edge> edges(E);
    cout << "Enter the source, destination, and weight for each edge:" << endl;
    for (int i = 0; i < E; ++i) {
        cin >> edges[i].src >> edges[i].dest >> edges[i].weight;
    }

    int src;
    cout << "Enter the source vertex: ";
    cin >> src;

    bellmanFord(edges, V, E, src);

    return 0;
}

上述C++代码中，Edge结构体表示图的边，bellmanFord函数实现了Bellman-Ford算法，其中distance数组存储了从源节点到各个节点的最短路径估计值。在算法结束后，它会输出从源节点到所有其他节点的最短路径。如果存在负权环，则会输出相应的提示。

Dijkstra算法

Dijkstra算法是一种用于解决单源最短路径问题的贪心算法。它通过不断选择距离源节点最近的节点来逐步确定最短路径。以下是Dijkstra算法的详细说明以及一个简单的C++实现。

💡 该算法要求所有边的权重都为非负值

Dijkstra算法简介：

Dijkstra算法的基本思想是维护一个集合，其中包含了已经找到最短路径的节点，以及一个数组用于存储从源节点到其他节点的最短路径估计值。在每一步，选择距离源节点最近的未标记节点，并通过这个节点更新其他节点的最短路径估计值。重复这个过程，直到找到从源节点到目标节点的最短路径或者所有节点都被标记。

算法步骤：

  1. 初始化：将源节点的最短路径估计值设为0，其他节点的最短路径估计值设为正无穷大。
  2. 在每一步中，选择未标记节点中距离源节点最近的节点，标记它，并更新通过这个节点到其他未标记节点的最短路径估计值。
  3. 重复步骤2，直到找到从源节点到目标节点的最短路径或者所有节点都被标记。

C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

struct Edge {
    int dest, weight;
};

class Graph {
public:
    int V; // Number of vertices
    vector<vector<Edge>> adj; // Adjacency list

    Graph(int V) {
        this->V = V;
        adj.resize(V);
    }

    void addEdge(int src, int dest, int weight) {
        Edge edge = {dest, weight};
        adj[src].push_back(edge);
    }

    void dijkstra(int src) {
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        vector<int> distance(V, INT_MAX);

        pq.push({0, src});
        distance[src] = 0;

        while (!pq.empty()) {
            int u = pq.top().second;
            pq.pop();

            for (const Edge& edge : adj[u]) {
                int v = edge.dest;
                int w = edge.weight;

                if (distance[u] != INT_MAX && distance[u] + w < distance[v]) {
                    distance[v] = distance[u] + w;
                    pq.push({distance[v], v});
                }
            }
        }

        // Print the result
        cout << "Shortest distances from source " << src << " to all other vertices:" << endl;
        for (int i = 0; i < V; ++i) {
            cout << "Vertex " << i << ": " << distance[i] << endl;
        }
    }
};

int main() {
    int V, E; // V is the number of vertices, E is the number of edges
    cout << "Enter the number of vertices and edges: ";
    cin >> V >> E;

    Graph graph(V);

    cout << "Enter the source, destination, and weight for each edge:" << endl;
    for (int i = 0; i < E; ++i) {
        int src, dest, weight;
        cin >> src >> dest >> weight;
        graph.addEdge(src, dest, weight);
    }

    int src;
    cout << "Enter the source vertex: ";
    cin >> src;

    graph.dijkstra(src);

    return 0;
}

上述C++代码中，Edge结构体表示图的边，Graph类封装了图的邻接列表和Dijkstra算法的实现。在算法结束后，它会输出从源节点到所有其他节点的最短路径。

链式前向星

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <queue>
#include <iostream>
using namespace std;
#define maxn (int)1e6 + 10
#define inf 2e9
#define ll long long
#define pr pair<int, int>
priority_queue<pr, vector<pr>, greater<pr>> q;
class edgex
{
public:
    int to;
    int next;
    int weight;
};
int head[maxn];
edgex edge[maxn * 2];
int cnt = 0;
void add(int u, int v, int w)
{
    edge[++cnt].next = head[u];
    edge[cnt].to = v;
    edge[cnt].weight = w;
    head[u] = cnt;
}
int dis[maxn];
bool visit[maxn];
int main()
{
    int n, m;
    cin >> n >> m;
    int u, v, w;
    for (int i = 1; i <= m; ++i)
    {
        cin >> u >> v >> w;
        add(u, v, w);
        add(v, u, w);
    }
    for (int i = 2; i <= n; ++i)
    {
        dis[i] = inf;
    }
    q.push(make_pair(0, 1));
    while (!q.empty())
    {
        auto it = q.top();
        q.pop();
        int num = it.second;
        if (visit[num])
        {
            continue;
        }
        visit[num] = true;
        for (int i = head[num]; i; i = edge[i].next)
        {
            int to = edge[i].to;
            int weight = edge[i].weight;
            dis[to] = min(dis[to], max(weight, dis[num]));
            q.push(make_pair(dis[to], to));
        }
    }
    for (int i = 2; i <= n; ++i)
    {
        if (dis[i] == inf)
        {
            cout << "-1\n";
        }
        else
        {
            cout << dis[i] << "\n";
        }
    }
}

第25章 所有节点对的最短路径问题

Floyd-Warshall算法

Floyd-Warshall算法是一种经典的图算法，用于求解所有点对之间的最短路径。该算法的时间复杂度为O(V3)(V^3)，其中V是图中顶点的数量。它基于动态规划的思想，适用于有向图或无向图，可以处理带有负权边但无负权环路的图。

动态规划的思路：

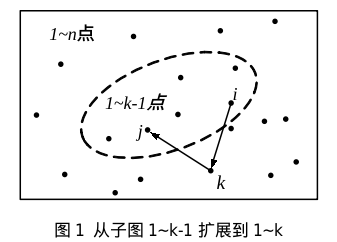
求图上两点 i、j 之间的最短距离，可以按“从小图到全图”的步骤，在逐步扩大图的过程中计算和更新最短路。想象图中的每个点是一个灯，开始时所有灯都是灭的。然后逐个点亮灯，每点亮一个灯，就重新计算 i、j 的最短路，要求路径只能经过点亮的灯。所有灯都点亮后，计算结束。在这个过程中，点亮第 k 个灯时，能用到 1∼k−1 个亮灯的结果。

定义状态为 dp[k][i][j]，i、j、k 是点的编号，范围 1∼n 。状态 dp[k][i][j] 表示在包含 1∼k 点的子图上，点对 i、j 之间的最短路。当从子图 1∼k−1 扩展到子图 1∼k 时，状态转移方程这样设计：

💡 dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])

Untitled

计算过程如上图所示，虚线圆圈内是包含了 1∼k−1 点的子图。方程中的 dp[k−1][i][j] 是虚线子图内的点对 i、j 的最短路；dp[k−1][i][k]+dp[k−1][k][j] 是经过 k 点的新路径的长度，即这条路径从 i 出发，先到 k，再从 k 到终点 j。比较不经过 k 的最短路径 dp[k−1][i][j] 和经过 k 的新路径，较小者就是新的 dp[k][i][j]。每次扩展一个新点 k 时，都能用到 1∼k−1 的结果，从而提高了效率。这就是**动态规划**的方法。
当 k 从 1 逐步扩展到 n 时，最后得到的 dp[n][i][j] 是点对 i、j 之间的最短路径长度。由于 i 和 j 是图中所有的点对，所以能得到所有点对之间的最短路。

算法步骤：

  1. 初始化：创建一个二维数组 dist[][] 用于存储节点之间的最短距离。初始化这个数组，使得 dist[i][j] 表示节点 i 到节点 j 的最短路径距离。如果两个节点之间有直接的边，则 dist[i][j] 设为这条边的权重值，否则设为一个较大的数或者无穷大。
  2. 进行迭代：使用三重循环遍历所有节点对 (i, j)，在每次迭代中尝试找到节点 k 作为中间节点，检查是否存在一条路径经过节点 k 使得从 i 到 j 的路径长度变短。更新 dist[i][j] 为 min(dist[i][j], dist[i][k] + dist[k][j])。

用邻接矩阵表示图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>
using namespace std;

#define INF 99999

vector<vector<int>> floydWarshall(vector<vector<int>>& graph, int V) {
    vector<vector<int>> dist = graph;

    for (int k = 0; k < V; k++) {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }

    return dist;
}

int main() {
    int V;
    cin >> V;

    vector<vector<int>> graph(V, vector<int>(V, INF));

    vector<vector<int>> dist = floydWarshall(graph, V);

    return 0;
}

这个示例首先接受用户输入图的节点数和邻接矩阵，然后使用 Floyd-Warshall 算法计算最短路径矩阵，并将结果输出。记得将输入的边权重矩阵中不存在的边表示为INF或者一个足够大的数。

C5 上机A题：（下面的代码还可以输出最短路径）

此题点的个数不多（不超过300），但是需要查询任意两点的最短距离，并且查询次数在10510^5，因此特别适合用Floyd-Warshall算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#define Max 303 // 最大点数

const unsigned long long INF = 1e12 + 1; // 权值最大为10^9，INF要开得比10^9大几个数量级

using namespace std;

struct AMGraph {						//定义邻接矩阵
	int vex, arc;
	unsigned long long arcs[Max][Max];
};

unsigned long long dis[Max][Max];
int  path[Max][Max];				//dis存最短路程，path保存路径
// path[i][j] = k表示从i到k经过的最后一个节点为k，可以递归path[i][k]求出完整路径
// 若k为-1表示i和j不连通
void Floyd(AMGraph &G)							//弗洛伊德算法
{
	for (int i = 1; i <= G.vex; i++)			//初始化dis和path
		for (int j = 1; j <= G.vex; j++)
		{
			dis[i][j] = G.arcs[i][j];
			if (dis[i][j] != INF&&i != j) path[i][j] = i;
			else path[i][j] = -1;
		}
			
	/***************Floyd核心算法****************/
	for(int k=1; k<=G.vex; k++)					//遍历每个点
		for(int i=1; i<=G.vex; i++)				//遍历每条边
			for (int j = 1; j <= G.vex; j++)
			{
				if (dis[i][k] + dis[k][j] < dis[i][j]) {	
					dis[i][j] = dis[i][k] + dis[k][j];			//松弛操作
					path[i][j] = k;								//保存j前驱结点k
				}
			}
}

void putin(AMGraph &G)							//输入图
{
	int u, v, w;
	
	cin >> G.vex >> G.arc;

	for (int i = 1; i <= G.vex; i++)			//初始化邻接矩阵
		for (int j = 1; j <= G.vex; j++)
		{
			if (i == j) G.arcs[i][j] = 0;
			else G.arcs[i][j] = INF;
		}

	for (int i = 0; i < G.arc; i++)
	{
		cin >> u >> v >> w;
        if(w < G.arcs[u][v])
		    G.arcs[u][v] = w;
//		G.arcs[v][u] = w;
	}
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
	AMGraph G;
	putin(G);
	Floyd(G);
    int q, u, v;
    cin >> q;
    while(q--){
        cin >> u >> v;
        if((u != v) && (path[u][v] == -1)){
            cout << -1 << endl;
        }
        else{
            cout << dis[u][v] << endl;
        }        
    }

	return 0;
}

第26章 最大流

EK（Edmond—Karp）算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <queue>
#include<string.h>
using namespace std;
#define arraysize 201
int maxData = 0x7fffffff;
int capacity[arraysize][arraysize]; //记录残留网络的容量
int flow[arraysize];                //标记从源点到当前节点实际还剩多少流量可用
int pre[arraysize];                 //标记在这条路径上当前节点的前驱,同时标记该节点是否在队列中
int n,m;
queue<int> myqueue;
int BFS(int src,int des)
{
    int i,j;
    while(!myqueue.empty())       //队列清空
        myqueue.pop();
    for(i=1;i<m+1;++i)
    {
        pre[i]=-1;
    }
    pre[src]=0;
    flow[src]= maxData;
    myqueue.push(src);
    while(!myqueue.empty())
    {
        int index = myqueue.front();
        myqueue.pop();
        if(index == des)            //找到了增广路径
            break;
        for(i=1;i<m+1;++i)
        {
            if(i!=src && capacity[index][i]>0 && pre[i]==-1)
            {
                 pre[i] = index; //记录前驱
                 flow[i] = min(capacity[index][i],flow[index]);   //关键：迭代的找到增量
                 myqueue.push(i);
            }
        }
    }
    if(pre[des]==-1)      //残留图中不再存在增广路径
        return -1;
    else
        return flow[des];
}
int maxFlow(int src,int des)
{
    int increasement= 0;
    int sumflow = 0;
    while((increasement=BFS(src,des))!=-1)
    {
         int k = des;          //利用前驱寻找路径
         while(k!=src)
         {
              int last = pre[k];
              capacity[last][k] -= increasement; //改变正向边的容量
              capacity[k][last] += increasement; //改变反向边的容量
              k = last;
         }
         sumflow += increasement;
    }
    return sumflow;
}
int main()
{
    int i,j;
    int start,end,ci;
    while(cin>>n>>m)
    {
        memset(capacity,0,sizeof(capacity));
        memset(flow,0,sizeof(flow));
        for(i=0;i<n;++i)
        {
            cin>>start>>end>>ci;
            if(start == end)               //考虑起点终点相同的情况
               continue;
            capacity[start][end] +=ci;     //此处注意可能出现多条同一起点终点的情况
        }
        cout<<maxFlow(1,m)<<endl;
    }
    return 0;
}

Ford-Fulkerson算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int map[300][300];
int used[300];
int n,m;
const int INF = 1000000000;
int dfs(int s,int t,int f)
{
    if(s == t) return f;
    for(int i = 1 ; i <= n ; i ++) {
        if(map[s][i] > 0 && !used[i]) {
            used[i] = true;
            int d = dfs(i,t,min(f,map[s][i]));
            if(d > 0) {
                map[s][i] -= d;
                map[i][s] += d;
                return d;
            }
        }
    }
}
int maxflow(int s,int t)
{
    int flow = 0;
    while(true) {
        memset(used,0,sizeof(used));
        int f = dfs(s,t,INF);//不断找从s到t的增广路
        if(f == 0) return flow;//找不到了就回去
        flow += f;//找到一个流量f的路
    }
}
int main()
{
    while(scanf("%d%d",&m,&n) != EOF) {
        memset(map,0,sizeof(map));
        for(int i = 0 ; i < m ; i ++) {
            int from,to,cap;
            scanf("%d%d%d",&from,&to,&cap);
            map[from][to] += cap;
        }
        cout << maxflow(1,n) << endl;
    }
    return 0;</span>
}

Dinic算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <cstdio>
#include <string.h>
#include <queue>
#include <iostream>
using namespace std;
int const inf = 0x7fffffff;
int const MAX = 105;
int n, m; 
int s, t;
long long c[MAX][MAX], dep[MAX];//dep[MAX]代表当前层数
 
int bfs(int s, int t)//重新建图，按层次建图
{
    queue<int> q;
    memset(dep, -1, sizeof(dep));
    dep[s] = 0;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int v = 1; v <= n; v++){
            if(c[u][v] > 0 && dep[v] == -1){//如果可以到达且还没有访问，可以到达的条件是剩余容量大于0，没有访问的条件是当前层数还未知
                dep[v] = dep[u] + 1;
                q.push(v);
            }
        }
    }
    return dep[t] != -1;
}
 
long long dfs(int u, long long mi, int t)//查找路径上的最小流量
{
    if(u == t)
        return mi;
    long long tmp;
    for(int v = 1; v <= n; v++){
        if(c[u][v] > 0 && dep[v] == dep[u] + 1  && (tmp = dfs(v, min(mi, c[u][v]), t))){
            c[u][v] -= tmp;
            c[v][u] += tmp;
            return tmp;
        }
    }
    return 0;
}
 
long long dinic(int s, int t)
{
    long long ans = 0, tmp;
    while(bfs(s, t)){
        while(1){
            tmp = dfs(s, inf, t);
            if(tmp == 0)
                break;
            ans += tmp;
        }
    }
    return ans;
}
 
int main()
{
    int T;
    cin >> T;
    while(T--){
        cin >> n >> m >> s >> t;
        
        memset(c, 0, sizeof(c));
        int u, v, w;
        while(m--){
            cin >> u >> v >> w;
            c[u][v] += w;
        }
        cout << dinic(s, t) << endl;
    }
    return 0;
}

算法问题选编

计算几何

基础模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <cstdio>
#include <cmath>

using namespace std;

const double pi = acos(-1.0);
const double inf = 1e100;
const double eps = 1e-6;
int sgn(double d){
    if(fabs(d) < eps)
        return 0;
    if(d > 0)
        return 1;
    return -1;
}
int dcmp(double x, double y){
    if(fabs(x - y) < eps)
        return 0;
    if(x > y)
        return 1;
    return -1;
}
int main() {
    double x = 1.49999;
    int fx = floor(x);//向下取整函数
    int cx = ceil(x);//向上取整函数
    int rx = round(x);//四舍五入函数
    printf("%f %d %d %d\n", x, fx, cx, rx);
    //输出结果 1.499990 1 2 1
    return  0 ;
}

💡 不要直接用等号判断浮点数是否相等！

  1. 误差判别法
1
2
3
4
5
6
7
8
const double eps = 1e-9;
int dcmp(double x, double y){
    if(fabs(x - y) < eps)
        return 0;
    if(x > y)
        return 1;
    return -1;
}
  1. 化浮为整

在不溢出整数范围的情况下，可以通过乘上10k10^k转化为整数运算，最后再将结果转化为浮点数输出

💡 输出时一定要小心不要输出 −0

点与向量

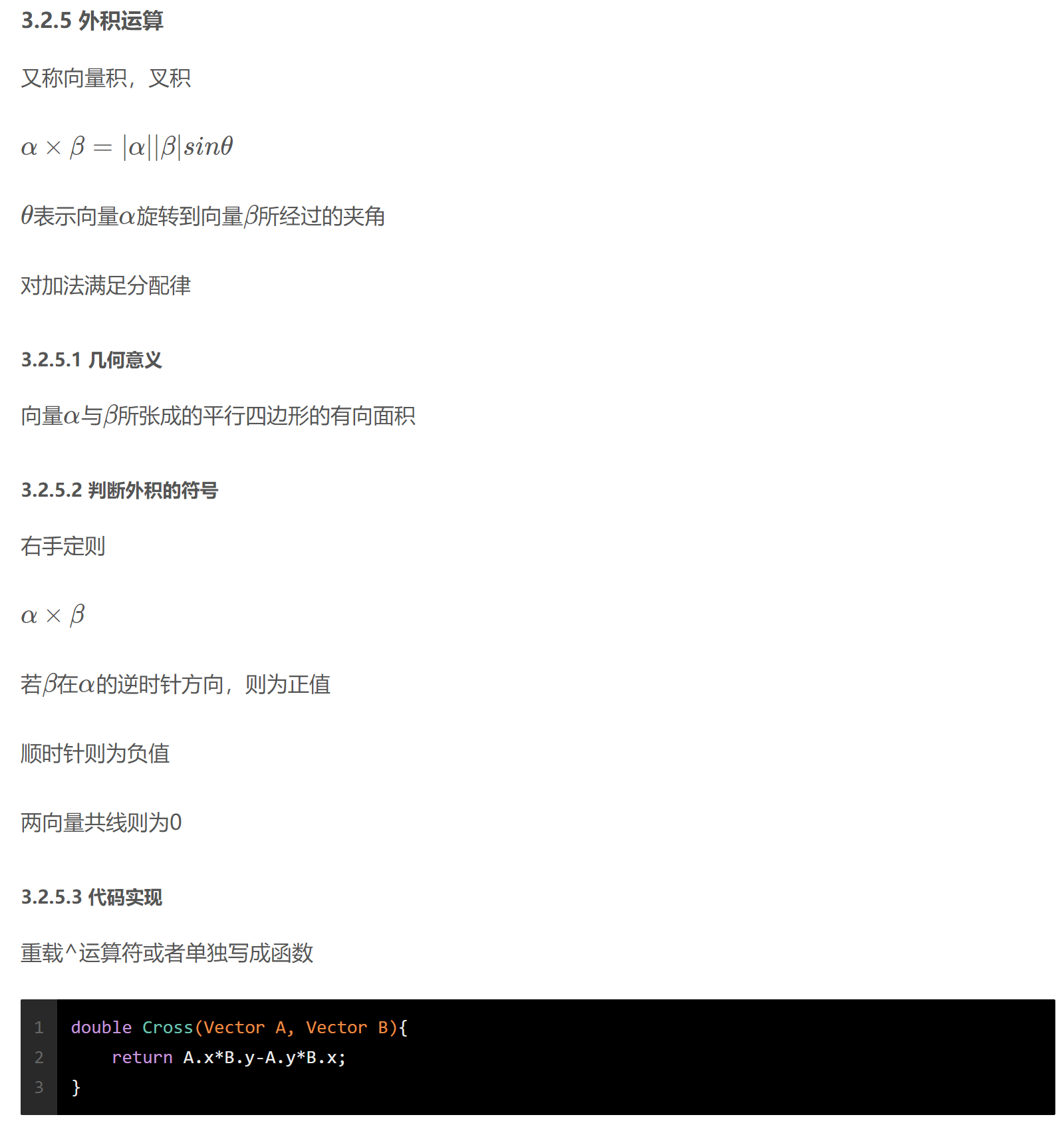
Untitled

Untitled

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
struct Point{
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;

Vector operator + (Vector A, Vector B){
    return Vector(A.x+B.x, A.y+B.y);
}
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
Vector operator * (Vector A, double p){
    return Vector(A.x*p, A.y*p);
}
Vector operator / (Vector A, double p){
    return Vector(A.x/p, A.y/p);
}
bool operator < (const Point& a, const Point& b){
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
const double eps = 1e-6;
int sgn(double x){
    if(fabs(x) < eps)
        return 0;
    if(x < 0)
        return -1;
    return 1;
}
bool operator == (const Point& a, const Point& b){
    if(sgn(a.x-b.x) == 0 && sgn(a.y-b.y) == 0)
        return true;
    return false;
}
double Dot(Vector A, Vector B){
    return A.x*B.x + A.y*B.y;
}
// 取模（长度）
double Length(Vector A){
    return sqrt(Dot(A, A));
}
double Angle(Vector A, Vector B){
    return acos(Dot(A, B)/Length(A)/Length(B));
}
double Cross(Vector A, Vector B){
    return A.x*B.y-A.y*B.x;
}
// 平行四边形有向面积
double Area2(Point A, Point B, Point C){
    return Cross(B-A, C-A);
}
// 逆时针旋转后的向量
Vector Rotate(Vector A, double rad){//rad为弧度 且为逆时针旋转的角
    return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
//计算向量逆时针旋转九十度的单位法向量
Vector Normal(Vector A){//向量A左转90°的单位法向量
    double L = Length(A);
    return Vector(-A.y/L, A.x/L);
}
// 判断折线bc→是不是向ab的逆时针方向（左边）转向
// 凸包构造时将会频繁用到此公式
bool ToLeftTest(Point a, Point b, Point c){
    return Cross(b - a, c - b) > 0;
}

点与线

Untitled

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
struct Line{//直线定义
    Point v, p;
    Line(Point v, Point p):v(v), p(p) {}
    Point point(double t){//返回点P = v + (p - v)*t
        return v + (p - v)*t;
    }
};
//计算两直线交点
//调用前需保证 Cross(v, w) != 0
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
    Vector u = P-Q;
    double t = Cross(w, u)/Cross(v, w);
    return P+v*t;
}
//点P到直线AB距离公式
double DistanceToLine(Point P, Point A, Point B){
    Vector v1 = B-A, v2 = P-A;
    return fabs(Cross(v1, v2)/Length(v1));
}//不去绝对值，得到的是有向距离
//点P到线段AB距离公式
double DistanceToSegment(Point P, Point A, Point B){
    if(A == B)
        return Length(P-A);
    Vector v1 = B-A, v2 = P-A, v3 = P-B;
    if(dcmp(Dot(v1, v2)) < 0)
        return Length(v2);
    if(dcmp(Dot(v1, v3)) > 0)
        return Length(v3);
    return DistanceToLine(P, A, B);
}
//点P在直线AB上的投影点
Point GetLineProjection(Point P, Point A, Point B){
    Vector v = B-A;
    return A+v*(Dot(v, P-A)/Dot(v, v));
}
//判断p点是否在线段a1a2上
bool OnSegment(Point p, Point a1, Point a2){
    return dcmp(Cross(a1-p, a2-p)) == 0 && dcmp(Dot(a1-p, a2-p)) < 0;
}
//判断两线段是否相交
bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2){
    double c1 = Cross(a2-a1, b1-a1), c2 = Cross(a2-a1, b2-a1);
    double c3 = Cross(b2-b1, a1-b1), c4 = Cross(b2-b1, a2-b1);
    //if判断控制是否允许线段在端点处相交，根据需要添加
    if(!sgn(c1) || !sgn(c2) || !sgn(c3) || !sgn(c4)){
        bool f1 = OnSegment(b1, a1, a2);
        bool f2 = OnSegment(b2, a1, a2);
        bool f3 = OnSegment(a1, b1, b2);
        bool f4 = OnSegment(a2, b1, b2);
        bool f = (f1|f2|f3|f4);
        return f;
    }
    return (sgn(c1)*sgn(c2) < 0 && sgn(c3)*sgn(c4) < 0);
}

多边形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//多边形有向面积
double PolygonArea(Point* p, int n){//p为端点集合，n为端点个数
    double s = 0;
    for(int i = 1; i < n-1; ++i)
        s += Cross(p[i]-p[0], p[i+1]-p[0]);
    return s;
}
//判断点是否在多边形内，若点在多边形内返回1，在多边形外部返回0，在多边形上返回-1
int isPointInPolygon(Point p, vector<Point> poly){
    int wn = 0;
    int n = poly.size();
    for(int i = 0; i < n; ++i){
        if(OnSegment(p, poly[i], poly[(i+1)%n])) return -1;
        int k = sgn(Cross(poly[(i+1)%n] - poly[i], p - poly[i]));
        int d1 = sgn(poly[i].y - p.y);
        int d2 = sgn(poly[(i+1)%n].y - p.y);
        if(k > 0 && d1 <= 0 && d2 > 0) wn++;
        if(k < 0 && d2 <= 0 && d1 > 0) wn--;
    }
    if(wn != 0)
        return 1;
    return 0;
}

圆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
struct Circle{ // 定义
    Point c;
    double r;
    Circle(Point c, double r):c(c), r(r) {}
    Point point(double a){//通过圆心角求坐标
        return Point(c.x + cos(a)*r, c.y + sin(a)*r);
    }
};
//求圆与直线交点
int getLineCircleIntersection(Line L, Circle C, double& t1, double& t2, vector<Point>& sol){
    double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
    double e = a*a + c*c, f = 2*(a*b + c*d), g = b*b + d*d - C.r*C.r;
    double delta = f*f - 4*e*g;//判别式
    if(sgn(delta) < 0)//相离
        return 0;
    if(sgn(delta) == 0){//相切
        t1 = -f /(2*e);
        t2 = -f /(2*e);
        sol.push_back(L.point(t1));//sol存放交点本身
        return 1;
    }
    //相交
    t1 = (-f - sqrt(delta))/(2*e);
    sol.push_back(L.point(t1));
    t2 = (-f + sqrt(delta))/(2*e);
    sol.push_back(L.point(t2));
    return 2;
}
// 两圆相交面积
// 通过计算两个圆相交所构成的两个扇形面积和减去其构成的筝形的面积
double AreaOfOverlap(Point c1, double r1, Point c2, double r2){
    double d = Length(c1 - c2);
    if(r1 + r2 < d + eps)
        return 0.0;
    if(d < fabs(r1 - r2) + eps){
        double r = min(r1, r2);
        return pi*r*r;
    }
    double x = (d*d + r1*r1 - r2*r2)/(2.0*d);
    double p = (r1 + r2 + d)/2.0;
    double t1 = acos(x/r1);
    double t2 = acos((d - x)/r2);
    double s1 = r1*r1*t1;
    double s2 = r2*r2*t2;
    double s3 = 2*sqrt(p*(p - r1)*(p - r2)*(p - d));
    return s1 + s2 - s3;
}

寻找凸包

Graham扫描法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
const int maxn = 1e3 + 5;
struct Point {
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;
Point lst[maxn];
int stk[maxn], top;
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
int sgn(double x){
    if(fabs(x) < eps)
        return 0;
    if(x < 0)
        return -1;
    return 1;
}
double Cross(Vector v0, Vector v1) {
    return v0.x*v1.y - v1.x*v0.y;
}
double Dis(Point p1, Point p2) { //计算 p1p2的 距离
    return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y));
}
bool cmp(Point p1, Point p2) { //极角排序函数 ，角度相同则距离小的在前面
    int tmp = sgn(Cross(p1 - lst[0], p2 - lst[0]));
    if(tmp > 0)
        return true;
    if(tmp == 0 && Dis(lst[0], p1) < Dis(lst[0], p2))
        return true;
    return false;
}
//点的编号0 ~ n - 1
//返回凸包结果stk[0 ~ top - 1]为凸包的编号
void Graham(int n) {
    int k = 0;
    Point p0;
    p0.x = lst[0].x;
    p0.y = lst[0].y;
    for(int i = 1; i < n; ++i) {
        if( (p0.y > lst[i].y) || ((p0.y == lst[i].y) && (p0.x > lst[i].x)) ) {
            p0.x = lst[i].x;
            p0.y = lst[i].y;
            k = i;
        }
    }
    lst[k] = lst[0];
    lst[0] = p0;
    sort(lst + 1, lst + n, cmp);
    if(n == 1) {
        top = 1;
        stk[0] = 0;
        return ;
    }
    if(n == 2) {
        top = 2;
        stk[0] = 0;
        stk[1] = 1;
        return ;
    }
    stk[0] = 0;
    stk[1] = 1;
    top = 2;
    for(int i = 2; i < n; ++i) {
        while(top > 1 && Cross(lst[stk[top - 1]] - lst[stk[top - 2]], lst[i] - lst[stk[top - 2]]) <= 0)
            --top;
        stk[top] = i;
        ++top;
    }
    return ;
}

Andrew算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
struct Point {
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
bool operator < (const Point& a, const Point& b){
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
double Cross(Vector v0, Vector v1) {
    return v0.x*v1.y - v1.x*v0.y;
}
//计算凸包，输入点数组为 p，个数为 n， 输出点数组为 ch。函数返回凸包顶点数
//如果不希望凸包的边上有输入点，则把两个 <= 改为 <
//在精度要求高时建议用dcmp比较
//输入不能有重复点，函数执行完后输入点的顺序被破坏
int ConvexHull(Point* p, int n, Point* ch) {
    sort(p, p+n);
    int m = 0;
    for(int i = 0; i < n; ++i) {
        while(m > 1 && Cross(ch[m-1] - ch[m-2], p[i] - ch[m-2]) < 0) {
            m--;
        }
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = n-2; i>= 0; --i) {
        while(m > k && Cross(ch[m-1] - ch[m-2], p[i] - ch[m-2]) < 0) {
            m--;
        }
        ch[m++] = p[i];
    }
    if(n > 1)
        --m;
    return m;
}

多项式与快速傅里叶变换

多项式与快速傅里叶变换（FFT）之间存在密切的关系，特别是在离散傅里叶变换（DFT）的计算中。FFT 是一种高效计算 DFT 的算法，而 DFT 又与多项式的乘法有关。

多项式

在代数中，一个多项式是由变量的幂和系数的有限和组成的表达式。例如，一个一元多项式：

P(x)=a0+a1x+a2x2+…+anxnP(x) = a_0 + a_1x + a_2x^2 + \ldots + a_nx^n

其中 a0,a1,…,ana_0, a_1, \ldots, a_n 是多项式的系数，xx 是变量。

离散傅里叶变换（DFT）

离散傅里叶变换将一个离散序列（通常是时域上的信号）转换为其在频域上的表示。对于一个 (N)-点序列 x0,x1,…,xN−1x_0, x_1, \ldots, x_{N-1}，其 DFT 定义如下：

Xk=∑n=0N−1xn⋅e−2πiNknX_k = \sum_{n=0}^{N-1} x_n \cdot e^{-\frac{2\pi i}{N}kn}

其中 XkX_k 是频域上的第 kk 个复数，ee 是自然对数的底，ii 是虚数单位。

快速傅里叶变换（FFT）

FFT 是一种高效计算 DFT 的算法，通过减少运算次数，从 O(N2)O(N^2) 的复杂度降低到 O(Nlog⁡N)O(N \log N)。FFT 的算法实现多种，其中最常见的是 Cooley-Tukey 算法。

FFT与多项式乘法

由于 DFT 与多项式的系数之间存在对应关系，FFT 被广泛用于多项式乘法。对于两个多项式 A(x)A(x) 和 B(x)B(x)，它们的乘积的系数可以通过计算它们的 DFT，相乘，再通过逆 DFT 得到。这样，可以将多项式的乘法复杂度从 O(n2)O(n^2)，降低到 O(nlog⁡n)O(n \log n)。

在这个例子中，multiply 函数用于计算两个多项式的卷积。你可以根据自己的需要调整输入多项式的系数。这段代码使用了复数类型 complex<double> 来表示复数，其中 real() 函数获取实部。最后，结果被四舍五入到最接近的整数。

对于更高效的迭代FFT，你可以使用位逆序置换（Bit-Reversal Permutation）来优化数据的存储和访问。以下是一个使用位逆序置换的迭代FFT的C++实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <iostream>
#include <cmath>
#include <vector>
#include <complex>
#include <algorithm>

using namespace std;

typedef complex<double> Complex;
const double PI = acos(-1.0);

// 位逆序置换
void bitReverse(vector<Complex>& a) {
    int n = a.size();
    int bits = log2(n);
    for (int i = 0; i < n; i++) {
        int j = 0;
        for (int bit = 0; bit < bits; bit++) {
            if (i & (1 << bit)) {
                j |= 1 << (bits - 1 - bit);
            }
        }
        if (j > i) {
            swap(a[i], a[j]);
        }
    }
}

// 迭代FFT
void iterativeFFT(vector<Complex>& a, bool invert) {
    int n = a.size();
    bitReverse(a);

    for (int len = 2; len <= n; len <<= 1) {
        double angle = 2 * PI / len * (invert ? -1 : 1);
        Complex wlen(cos(angle), sin(angle));

        for (int i = 0; i < n; i += len) {
            Complex w(1);
            for (int j = 0; j < len / 2; j++) {
                Complex u = a[i + j];
                Complex v = w * a[i + j + len / 2];
                a[i + j] = u + v;
                a[i + j + len / 2] = u - v;
                w *= wlen;
            }
        }
    }

    if (invert) {
        for (int i = 0; i < n; i++) {
            a[i] /= n;
        }
    }
}

// 多项式卷积
vector<int> multiply(const vector<int>& a, const vector<int>& b) {
    vector<Complex> fa(a.begin(), a.end()), fb(b.begin(), b.end());
    int n = 1;
    while (n < max(a.size(), b.size())) n <<= 1;
    n <<= 1;
    fa.resize(n);
    fb.resize(n);

    iterativeFFT(fa, false);
    iterativeFFT(fb, false);

    for (int i = 0; i < n; i++) {
        fa[i] *= fb[i];
    }

    iterativeFFT(fa, true);

    vector<int> result(n);
    for (int i = 0; i < n; i++) {
        result[i] = round(fa[i].real());
    }

    return result;
}

int main() {
    vector<int> a = {1, 2, 3}; // 第一个多项式系数
    vector<int> b = {4, 5, 6}; // 第二个多项式系数

    vector<int> result = multiply(a, b);

    cout << "Result of convolution: ";
    for (int i : result) {
        cout << i << " ";
    }
    cout << endl;

    return 0;
}

在这个实现中，bitReverse 函数用于执行位逆序置换，然后在迭代FFT的过程中使用这个置换后的数据。这有助于提高数据存储和访问的效率。

字符串匹配

1.朴素字符串匹配算法（Naive String Matching）：

也称为暴力匹配算法，它从文本的第一个字符开始与模式的第一个字符匹配，然后逐个字符比较，直到找到匹配或遍历完整个文本。

2. **Rabin-Karp算法：**基于哈希的字符串匹配算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <string>
#include <cmath>

using namespace std;

const int prime = 101;  // 选择一个较大的质数作为哈希函数的模

// 计算字符串的哈希值
int calculateHash(const string& str, int length) {
    int hash = 0;
    for (int i = 0; i < length; ++i) {
        hash += (int)str[i] * pow(prime, i);
    }
    return hash;
}

// 更新哈希值，用于滑动窗口
int recalculateHash(int oldHash, char oldChar, char newChar, int length) {
    return (oldHash - oldChar + newChar * pow(prime, length - 1)) * prime;
}

// Rabin-Karp算法实现
void rabinKarpSearch(const string& pattern, const string& text) {
    int patternLength = pattern.length();
    int textLength = text.length();
    int patternHash = calculateHash(pattern, patternLength);
    int textHash = calculateHash(text, patternLength);

    for (int i = 0; i <= textLength - patternLength; ++i) {
        if (patternHash == textHash) {
            // 如果哈希值相等，可能找到了匹配，进一步检查字符是否真的匹配
            bool match = true;
            for (int j = 0; j < patternLength; ++j) {
                if (pattern[j] != text[i + j]) {
                    match = false;
                    break;
                }
            }

            if (match) {
                cout << "Pattern found at index " << i << endl;
            }
        }

        // 更新哈希值，准备检查下一个子串
        if (i < textLength - patternLength) {
            textHash = recalculateHash(textHash, text[i], text[i + patternLength], patternLength);
        }
    }
}

int main() {
    string text = "ABABCABABABCABCABABC";
    string pattern = "ABABC";

    cout << "Text: " << text << endl;
    cout << "Pattern: " << pattern << endl;

    rabinKarpSearch(pattern, text);

    return 0;
}

3. 有限自动机法：

有限状态自动机（Finite State Machine，FSM）是一种用于字符串匹配的有效算法。在这种算法中，模式字符串被预处理成一个有限状态自动机，然后利用该自动机在文本中进行匹配。以下是有限状态自动机字符串匹配算法（Aho-Corasick算法）的简要说明和C++实现：

Aho-Corasick算法

Aho-Corasick算法是一种多模式字符串匹配算法，它可以同时搜索多个模式串。

基本思想：
  1. 构建Trie树：将所有模式串构建成一个Trie树，每个节点表示一个字符，从根节点到叶子节点的路径表示一个模式串。
  2. 添加失败路径（Failure Function）：为Trie树中的每个节点添加失败路径，使得在匹配失败时能够跳转到Trie树中的其他位置。
  3. 匹配过程：在文本串中按顺序遍历字符，并根据Trie树进行匹配，利用失败路径实现快速跳转。
C++实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <iostream>
#include <queue>
#include <unordered_map>

using namespace std;

class TrieNode {
public:
    unordered_map<char, TrieNode*> children;
    TrieNode* fail;
    bool isEnd;

    TrieNode() : fail(nullptr), isEnd(false) {}
};

class AhoCorasick {
public:
    TrieNode* root;

    AhoCorasick() : root(new TrieNode()) {}

    // 添加模式串到Trie树
    void addPattern(const string& pattern) {
        TrieNode* node = root;
        for (char c : pattern) {
            if (node->children.find(c) == node->children.end()) {
                node->children[c] = new TrieNode();
            }
            node = node->children[c];
        }
        node->isEnd = true;
    }

    // 构建失败路径
    void buildFailureFunction() {
        queue<TrieNode*> q;
        for (auto& kv : root->children) {
            kv.second->fail = root;
            q.push(kv.second);
        }

        while (!q.empty()) {
            TrieNode* curr = q.front();
            q.pop();

            for (auto& kv : curr->children) {
                char symbol = kv.first;
                TrieNode* child = kv.second;
                q.push(child);

                TrieNode* failure = curr->fail;
                while (failure != nullptr && failure->children.find(symbol) == failure->children.end()) {
                    failure = failure->fail;
                }

                if (failure != nullptr) {
                    child->fail = failure->children[symbol];
                } else {
                    child->fail = root;
                }
            }
        }
    }

    // 在文本中匹配模式串
    void match(const string& text) {
        TrieNode* node = root;

        for (int i = 0; i < text.size(); ++i) {
            char c = text[i];

            while (node != nullptr && node->children.find(c) == node->children.end()) {
                node = node->fail;
            }

            if (node == nullptr) {
                node = root;
            } else {
                node = node->children[c];

                // 打印匹配的模式串
                printMatches(node, i);
            }
        }
    }

    // 打印匹配的模式串
    void printMatches(TrieNode* node, int endIndex) {
        while (node != nullptr) {
            if (node->isEnd) {
                cout << "Pattern found at index " << endIndex << endl;
            }
            node = node->fail;
        }
    }
};

int main() {
    AhoCorasick ac;
    ac.addPattern("he");
    ac.addPattern("she");
    ac.addPattern("his");
    ac.addPattern("hers");

    ac.buildFailureFunction();

    string text = "ahishers";
    ac.match(text);

    return 0;
}

这是一个简单的Aho-Corasick算法的实现，可以根据实际需要进行优化和扩展。

4. KMP算法

KMP（Knuth-Morris-Pratt）算法是一种高效的字符串匹配算法，它通过利用已经匹配过的信息来避免不必要的字符比较。以下是KMP算法的简要说明和C++实现：

KMP算法

基本思想：
  1. 构建部分匹配表（Partial Match Table，PMT）：PMT记录了每个前缀的最长相等的真前缀和真后缀的长度。
  2. 利用PMT进行匹配：在匹配过程中，当发生不匹配时，根据PMT找到一个合适的位置跳过一部分字符。
C++实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <vector>

using namespace std;

// 构建部分匹配表（Partial Match Table）
vector<int> buildPMT(const string& pattern) {
    int patternLength = pattern.size();
    vector<int> pmt(patternLength, 0);

    int length = 0;
    int i = 1;

    while (i < patternLength) {
        if (pattern[i] == pattern[length]) {
            length++;
            pmt[i] = length;
            i++;
        } else {
            if (length != 0) {
                length = pmt[length - 1];
            } else {
                pmt[i] = 0;
                i++;
            }
        }
    }

    return pmt;
}

// KMP算法实现
void kmpSearch(const string& pattern, const string& text) {
    int patternLength = pattern.size();
    int textLength = text.size();

    // 构建部分匹配表
    vector<int> pmt = buildPMT(pattern);

    int i = 0;  // 索引用于遍历text
    int j = 0;  // 索引用于遍历pattern

    while (i < textLength) {
        if (pattern[j] == text[i]) {
            i++;
            j++;
        }

        if (j == patternLength) {
            cout << "Pattern found at index " << i - j << endl;
            j = pmt[j - 1];
        } else if (i < textLength && pattern[j] != text[i]) {
            if (j != 0) {
                j = pmt[j - 1];
            } else {
                i++;
            }
        }
    }
}

int main() {
    string text = "ABABDABACDABABCABAB";
    string pattern = "ABABC";

    cout << "Text: " << text << endl;
    cout << "Pattern: " << pattern << endl;

    kmpSearch(pattern, text);

    return 0;
}

这是一个简单的KMP算法的实现示例，用于在文本中查找模式串的出现。这个算法通过构建部分匹配表来提高匹配效率。在实际应用中，可以根据需要进行适当的优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 教材实现：
vector<int> computePrefix(const string& pattern) {
    int m = pattern.size();
    vector<int> pi(m, 0);
    int k = 0;
    for(int i = 1; i < m; i++) {
        while(k > 0 && pattern[k] != pattern[i]) {
            k = pi[k - 1];
        }
        if(pattern[k] == pattern[i]){
            k = k + 1;
        }
        pi[i] = k;
    }
    return pi;
}

void KMP-MATCHER()